Answer variants:
Sum of opposite angles of a cyclic quadrilateral is \(180^{\circ}\).
Angle in a semicircle is \(90^{\circ}\)
Sum of the two acute angles in a right-angled triangle is \(90^{\circ}\)
The linear pair of angles are always supplementary
Angles in the same segment are equal.
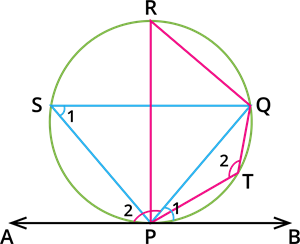
In the figure, prove that the angles with equal numbers are equal.
Answer the following with suitable theorems:
Angles | Theorems |
| \(\angle RQP\) \(=\) \(90^{\circ}\) | |
| \(\angle QRP\) \(+\) \(\angle RPQ\) \(=\) \(90^{\circ}\) | |
| \(\angle QRP\) \(=\) \(\angle PSQ\) | |
| \(\angle QPA\) \(+\) \(\angle QPB\) \(=\) \(180^{\circ}\) | |
| \(\angle PSQ\) \(+\) \(\angle PTQ\) \(=\) \(180^{\circ}\) |